Мы уже рассматривали типовые эпюры и построение эпюры консольной балки.
В этой статье мы рассмотрим как построить эпюру однопролетной шарнирно-опертой балки.
Эпюра однопролетной балки строится также ка эпюра консоли с той лишь разницей, что для определения опорных реакций необходимо решить систему уравнений. После нахождения опорных реакций метод построения эпюры аналогичен описанной в статье «Построение эпюр консольной балки».
Давайте рассмотрим построение эпюры балки на данном примере:
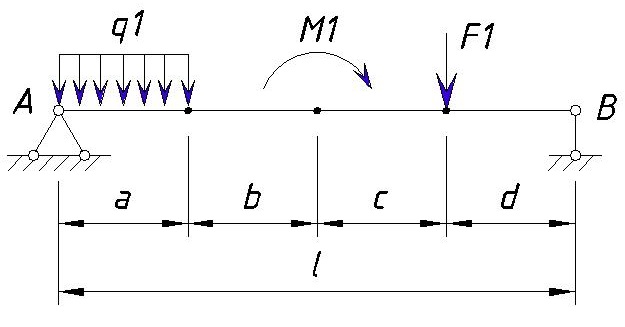
Значения нагрузок:
q1=20 кН/м
M1=10 кН·м
F1=30 кН
Расстояния между точками равны т,е. a=b=c=d=1м
Опорные реакции
Чтобы вычислить опорные реакции необходимо решить систему уравнений
Т.к. система неподвижна, а узлы вокруг точки A и B шарнирные, то сумма изгибающих моментов вокруг точек A и B равны нулю (если одна или обе опоры жестко закреплены, то это условие не работает и этот способ нахождения опорных реакций не работает).
![]()
Давайте обозначим опорные реакции в узлах крепления балки
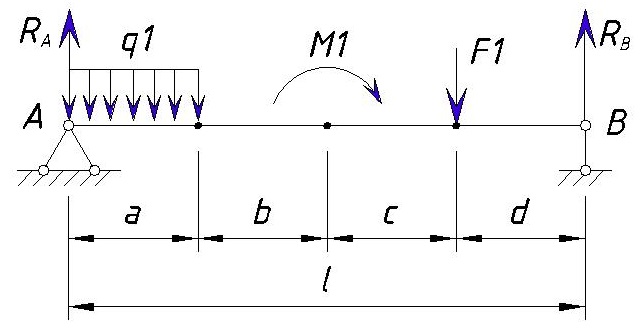
Опорных изгибающих моментов в точках A и B нет, да и на эпюрах изгибающий момент в данных точках должен быть равен нулю (может быть не равен нулю только если в этом узле прикладывается изгибающий момент или балка многопролетная/с жестким соединением в узле).
Давайте напишем условие равенства изгибающих моментов относительно точки A
![]()
Реакции опоры Ra нет в уравнении т.к. плечо приложения нагрузки равно нулю, поэтому он не создает изгибающий момент в этой точке.
Из уравнения, приведенного выше, мы можем вычислить реакцию Rb:

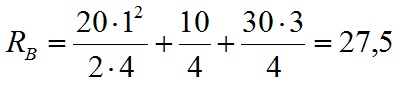
Теперь напишем уравнение равенства изгибающих моментов вокруг точки B
![]()
Из уравнения находим значение опорной реакции Ra:
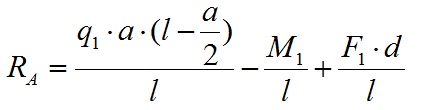
![]()
Вычисленные значения опорных реакций необходимо проверить по формуле:
![]()
![]()
Равенство верно, поэтому значение опорных реакция мы нашли правильно.
Назначение контрольных точек
Чтобы построить эпюру изгибающих моментов балки важно правильно определить все контрольные точки, для которых мы будем вычислять значения напряжения. Прежде всего это будут все точки, в которых приложена нагрузка, а также начинается или заканчивается равномерно-распределенная нагрузка. Также надо рассмотреть точки, в которых эпюра Q принимает значение равное нулю — в этой точке изгибающий момент может принимать максимальное значение (вы можете увидеть это на примере 2-х пролетной балки, рассмотренной в статье «Построение эпюр балки»).
Для начала мы назначим точки только в точках приложения нагрузки, в начале и конце приложения равномерно-распределенной нагрузки, но после построения эпюры Q может добавится еще точки для построения эпюры M.
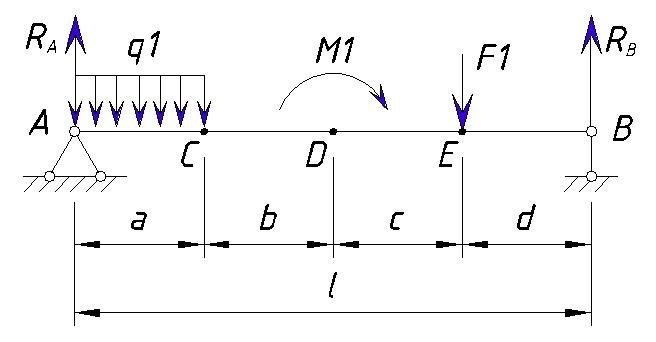
Построение эпюры Q (поперечной силы)
Я уже рассматривал построение эпюры Q для консольной балки в статье «Построение эпюр консольной балки», для построения эпюры поперечной силы одно-пролетной балки мы пользуемся тем же методом.
Эпюру Q мы строим перемещаясь от точки A в сторону точки B вычисляя значение поперечной силы в каждой точке и строя график в зависимости от вида нагрузки, приложенной к данному участку.
Для точки, в которой приложена сосредоточенная сила F нужно вычислить значение слева от точки (без учета этой силы) и справа (с учетом этой силы). В этой точке будет скачок поперечной силы. В остальных случаях поперечная сила изменяется прямолинейно (для равномерно-распределенной) или по кривой (для переменной нагрузки).
Не забываем про правило знаков:
Если внешняя нагрузка, приложенная к рассматриваемой части, стремится повернуть сечение на заданном участке по часовой стрелке, то значение будет положительным и откладывается вверх.
Если внешняя нагрузка стремится повернуть сечение на заданном участке против часовой стрелки, то значение будет отрицательным и откладывается вниз.
Определяем напряжения Q на участке AC
Значение поперечной силы в точке А равно значению опорной реакции Ra, которое мы вычислили ранее. Не забываем про правило знаков — если сила стремится повернуть рассматриваемый участок по часовой стрелке, то значение принимается со знаком плюс, если против часовой, то со знаком минус. Мы как-бы откидываем закрепление балки в точке А, заменив ее силой Ra, и закрепляем в точке C. Сила Ra стремится повернуть участок вокруг точки C по часовой стрелке, поэтому Ra принимается со знаком плюс.
![]()
На участке AC действует равномерно-распределенная нагрузка q1. Нагрузка q1 стремится повернуть рассматриваемый участок против часовой стрелки, поэтому данная нагрузка принимается со знаком минус. Рассчитываем значение поперечной силы в точке C
![]()
На участке AC нагрузка изменяется прямолинейно, поэтому эпюра Q на участке AC выглядит следующим образом:
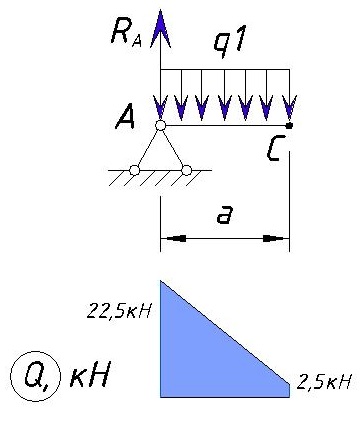
Определяем напряжения Q на участке CD
На участке CD нет нагрузки, поэтому значение поперечной силы на данном участке не изменяется. В точке D приложен изгибающий момент, но он не влияет на поперечную силу (влияние момента на поперечную силу отражено в реакции опоры). Поэтому значение Q в точке D равно:
![]()
На участке CD значение не Q не изменилось, поэтому эпюра Q выглядит следующим образом:
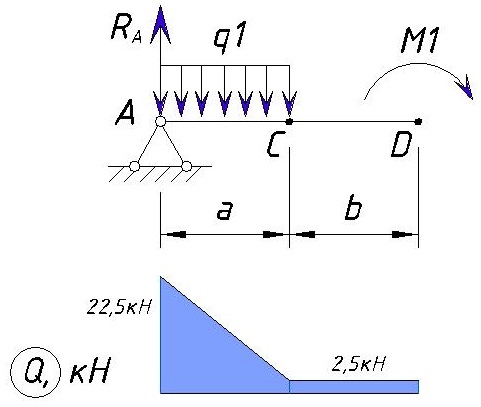
Определяем напряжения Q на участке DE
На участке DE нет нагрузок, поэтому значение Q не изменяется. В самой точке E приложена сосредоточенная сила F1, т.е. справа от точки E будет скачок поперечной силы на величину F, сила F будет со знаком минус т.к. она стремится повернуть сечение против часовой стрелки (относительно точки E справа).
![]()
![]()
Эпюра на участке DE будет выглядеть следующим образом:
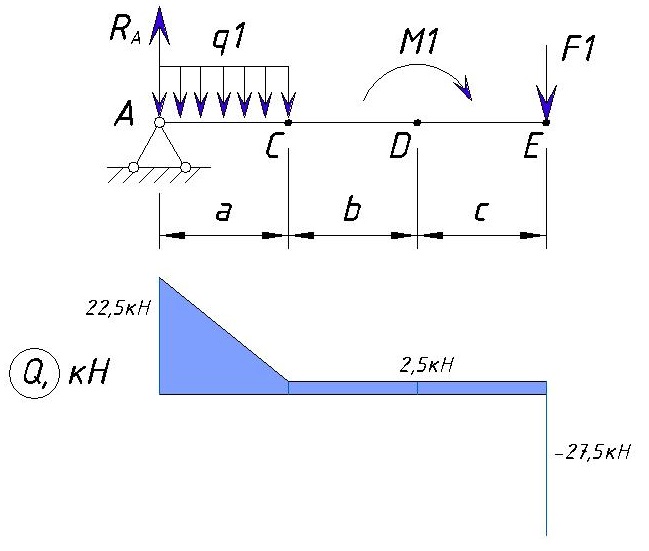
Определяем напряжения Q на участке EB
На участке нет нагрузок, поэтому напряжение на участке не изменяется. В самой точке B эпюра Q должна быть равна -Rb, что мы и видим
![]()
Итоговая эпюра Q
Построим эпюру Q на основе всех этих данных
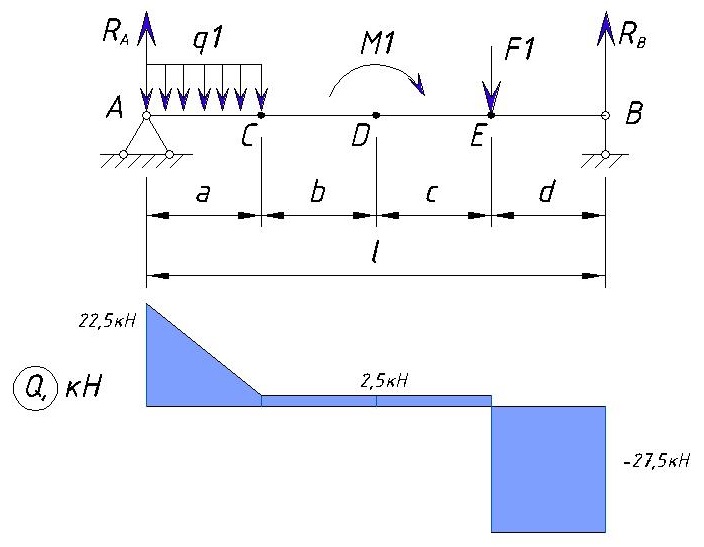
Эпюра в конце балки должна быть равна -Rb, что мы и имеем. То, что значение эпюры Q имеет знак минус в точке B не значит, что тут сечение растянуто, здесь сечение также сжато, но по правилу знаков значение отрицательное т.к. сил которые стремятся повернуть сечение против часовой стрелки больше чем сил стремящихся повернуть по часовой.
Можно отметить следующие закономерности при построении эпюры Q:
1) На участке приложения равномерно-распределенной нагрузки значение поперечной силы изменяется прямолинейно
2) На участке приложения переменной нагрузки изменение поперечной силы криволинейно
3) В точках приложения сосредоточенной силы эпюра Q имеет скачок напряжения
4) Изгибающий момент сам по себе не влияет на поперечную силу, но он воздействует на опорную реакцию, что конечно создает поперечное напряжение в балке
Построение эпюры M (изгибающих моментов)
Эпюра изгибающих моментов строится по тому же принципу, что описан в статье «Построение эпюр консольной балки».
Для построения эпюры М мы используем те же контрольные точки и те же участки, что мы использовали при построении эпюры Q.
Последовательно передвигаясь от точки А к точке B мы вычисляем значения моментов в контрольных точках и соединяем их в график который и будет указывать изгибающий момент в любой точке балки.
Изгибающий момент вычисляется произведением силы или центра приложения силы на плечо.
Для сосредоточенной силы мы умножаем значение нагрузки на расстояние до рассматриваемой точки. На графике эпюра M от действия сосредоточенной силы имеет прямую линию.
Чтобы определить изгибающий момент от действия равномерно-распределенной нагрузки определяем расстояние до середины рассматриваемого участка равномерно-распределенной нагрузки, умножаем на длину рассматриваемого участка и на величину нагрузки. На графике эпюра М от действия равномерно-распределенной нагрузки напоминает изогнутую линию, гиперболу.
Для переменной нагрузки изгибающий момент определяем следующим образом: определяется центр приложения нагрузки (длина приложения нагрузки делится в соотношении 1/3-2/3, центр приложения нагрузки находится ближе к максимальной нагрузке), определяем длину от этой точки до рассматриваемой, умножаем на длину приложения нагрузки, и умножаем на половину от приложенной нагрузки (q).На графике эпюра М от действия переменной нагрузки также как и для равномерно-распределенной напоминает изогнутую линию, но с большим изгибом.
Приложенный момент в точке просто суммируется с вычисляемым изгибающим моментом от других нагрузок. В точке где приложен момент эпюра совершает скачок. Значение момента не умножается на расстояние, а остается неизменным по всей длине.
Правило знаков для построения эпюры M
Тут есть 2-а метода: метод которым пользуются строители и метод, которым пользуются машиностроители.
У строителей изгибающий момент считается положительным, если внешняя нагрузка приводит к растяжению верхних волокон и график откладываем вверх. Если внешняя нагрузка приводит к растяжению нижних волокон, то изгибающий момент считается отрицательным и график откладывается вверх. Т.е. график всегда откладывается в сторону растянутых волокон.
У машиностроителей все наоборот — положительное значение откладывается в сторону сжатых волокон.
Ни в том, ни в другом случае ошибки нет, просто разные методы и итоговые значения будут одинаковыми, только знаки противоположными.
Не могу с уверенностью сказать почему у строителей изгибающий момент направлен в сторону растянутых волокон. Возможно из-за того, что при данном рассмотрении эпюра моментов во многих случаях повторяет изгиб балки.
Мы будем рассматривать метод, которым пользуются строители.
Определяем напряжения M на участке AC
Рассмотрим участок от точки A до точки C.
Значение изгибающего момента в точке A равно нулю, в точке B тоже равно нулю т.к. мы имеем однопролетную шарнирно-опертую балку.
![]()
На значение изгибающего момента в точке C влияют следующие силы:
1) Опорная реакция Ra. Действие силы растягивает нижние волокна (если рассматривать силу Ra вокруг точки C), поэтому значение изгибающего момента учитывается со знаком минус. Значение изгибающего момента от действия силы Ra равно произведению этой силы на плечо (расстояние от A до C в данном случае)
2) Равномерно-распределенная нагрузка q1. Действие силы растягивает верхние волокна, поэтому значение изгибающего момента от действия нагрузки q1 принимается со знаком плюс. Значение изгибающего момента от действия равномерно-распределенной нагрузки q1 равно произведению значения этой нагрузки (q1*a) на плечо (расстояние от центра равномерно-распределенной нагрузки до заданной точки, в данном случае a/2)
Вычислим значения изгибающего момента в точке C:
Т.к. на данном участке действует равномерно-распределенная нагрузка, то форма эпюры M на данном участке имеет изгиб в сторону действия нагрузки. Эпюра M на данном участке будет выглядеть следующим образом:
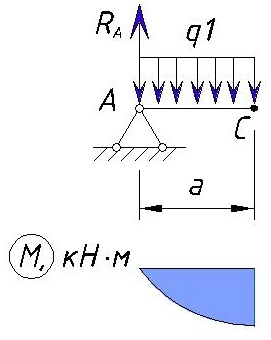
Определяем напряжения M на участке CD
На участке между точками C и D нет никаких нагрузок, а в точке D приложен изгибающий момент M1, поэтому необходимо считать вначале значение изгибающего момента без учета M1 (точка D слева), затем считать с учетом изгибающего момента M1 (точка D справа). На эпюре в точке D будет скачок напряжения изгибающих моментов.
На значение изгибающего момента в точке D влияют следующие силы:
1) Опорная реакция Ra. Действие силы растягивает нижние волокна (если рассматривать силу Ra вокруг точки D), поэтому значение изгибающего момента учитывается со знаком минус. Значение изгибающего момента от действия силы Ra равно произведению этой силы на плечо (расстояние от A до D в данном случае)
2) Равномерно-распределенная нагрузка q1. Действие силы растягивает верхние волокна, поэтому значение изгибающего момента от действия нагрузки q1 принимается со знаком плюс. Значение изгибающего момента от действия равномерно-распределенной нагрузки q1 равно произведению значения этой нагрузки (q1*a) на плечо (расстояние от центра равномерно-распределенной нагрузки до заданной точки, в данном случае a/2+b)
3) Изгибающий момент M1. Значение изгибающего момента не зависит от расстояния до нагрузки. Для расчета необходимо вначале рассчитать значение слева от точки где приложен данный момент, не учитывая его, и справа с учетом действия этого момента. Т.к. изгибающий момент растягивает нижние волокна, то учитываем его со знаком минус.
Вычислим значение изгибающего момента в точке D слева:
![]()
![]()
Вычислим значение изгибающего момента в точке D справа:
![]()
![]()
Эпюра M между точками C и D изменяется прямолинейно т.к. между этими нет сил. Эпюра на этом участке выглядит следующим образом:
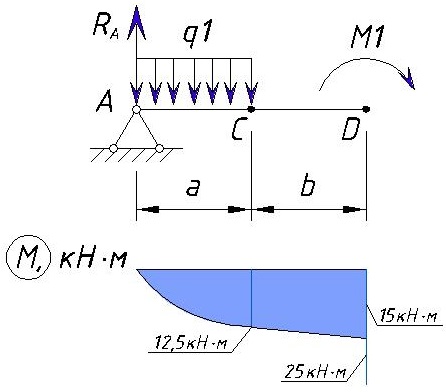
Определяем напряжения M на участке DE
На участке между точками D и E нет никаких нагрузок, а в точке E приложена сосредоточенная нагрузка F1, но т.к. плечо в данной точке равно нулю, то и изгибающий момент сила F не создает в точке E.
На значение изгибающего момента в точке E влияют следующие силы:
1) Опорная реакция Ra. Действие силы растягивает нижние волокна (если рассматривать силу Ra вокруг точки E), поэтому значение изгибающего момента учитывается со знаком минус. Значение изгибающего момента от действия силы Ra равно произведению этой силы на плечо (расстояние от A до E в данном случае)
2) Равномерно-распределенная нагрузка q1. Действие силы растягивает верхние волокна, поэтому значение изгибающего момента от действия нагрузки q1 принимается со знаком плюс. Значение изгибающего момента от действия равномерно-распределенной нагрузки q1 равно произведению значения этой нагрузки (q1*a) на плечо (расстояние от центра равномерно-распределенной нагрузки до заданной точки, в данном случае a/2+b+c)
3) Изгибающий момент M1. Значение изгибающего момента не зависит от расстояния до нагрузки. Для расчета необходимо вначале рассчитать значение слева от точки где приложен данный момент, не учитывая его, и справа с учетом действия этого момента. Т.к. изгибающий момент растягивает нижние волокна, то учитываем его со знаком минус.
Вычислим значение изгибающего момента в точке E:
![]()
![]()
Эпюра M между точками D и E изменяется линейно т.к. между этими нет сил. Эпюра на этом участке выглядит следующим образом:
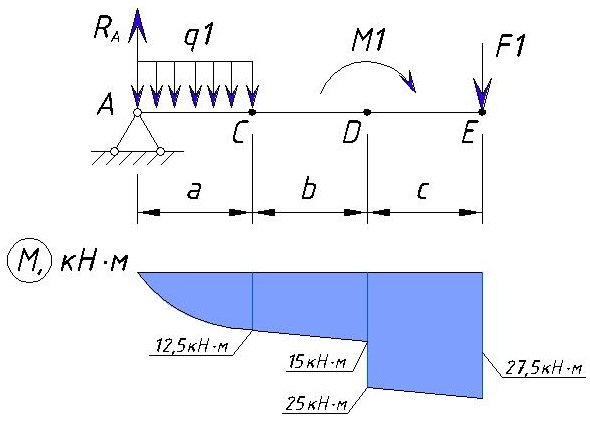
Определяем напряжения M на участке EB
На участке между точками E и B нет никаких нагрузок, а в точке B приложена опорная нагрузка Rb, но т.к. плечо в данной точке равно нулю, то и изгибающий момент опорная сила Rb не создает.
Изгибающий момент в точке B должен быть равен нулю, мы это сейчас проверим.
На значение изгибающего момента в точке B влияют следующие силы:
1) Опорная реакция Ra. Действие силы растягивает нижние волокна (если рассматривать силу Ra вокруг точки E), поэтому значение изгибающего момента учитывается со знаком минус. Значение изгибающего момента от действия силы Ra равно произведению этой силы на плечо (расстояние от A до B в данном случае)
2) Равномерно-распределенная нагрузка q1. Действие силы растягивает верхние волокна, поэтому значение изгибающего момента от действия нагрузки q1 принимается со знаком плюс. Значение изгибающего момента от действия равномерно-распределенной нагрузки q1 равно произведению значения этой нагрузки (q1*a) на плечо (расстояние от центра равномерно-распределенной нагрузки до заданной точки, в данном случае a/2+b+c+d)
3) Изгибающий момент M1. Значение изгибающего момента не зависит от расстояния до нагрузки. Для расчета необходимо вначале рассчитать значение слева от точки где приложен данный момент, не учитывая его, и справа с учетом действия этого момента. Т.к. изгибающий момент растягивает нижние волокна, то учитываем его со знаком минус.
4) Сила F1. Действие силы растягивает верхние волокна, поэтому учитывается со знаком плюс. Плечо действия силы равно d.
Вычислим значение изгибающего момента в точке B:
![]()
![]()
В принципе это тоже самое уравнение, которое мы решали при определении опорных реакций.
Т.к. на участке EB нет никаких нагрузок, то изменение изгибающего момента происходит прямолинейно.
Итоговая эпюра M
Теперь нарисуем всю эпюру M для данного примера
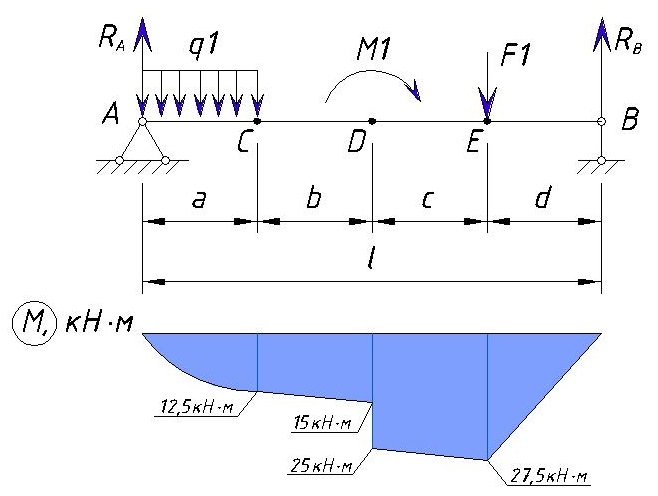
Можно отметить следующие правила при построении эпюры изгибающих моментов:
1) на участке приложения равномерно-распределенной или переменной нагрузки эпюра имеет изгиб
2) на участках где не приложены силы эпюра изменяется прямолинейно
3) в точке где приложен изгибающий момент происходит скачок напряжения
Итоговая эпюра Q и M
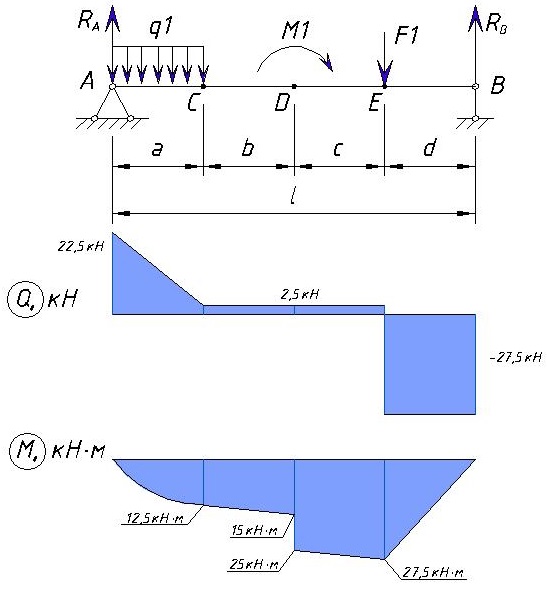
Удачи в учебе.
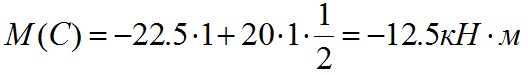
МОМЕНТ ВЫГНУТ НА ВСТРЕЧУ НАГРУЗКЕ
Уже много раз писал что есть 2-а метода — строители делают наоборот. Это не является ошибкой, просто другой принцип.
очень ценный материал, четко всё систематизировано, все понятно. спасибо, кстати, строителям всегда нужно знать где нахаодятся расстянутые волокна, чтобы знать где армировать, т.к. основные элементы в строительстве — жб балки и колонны.