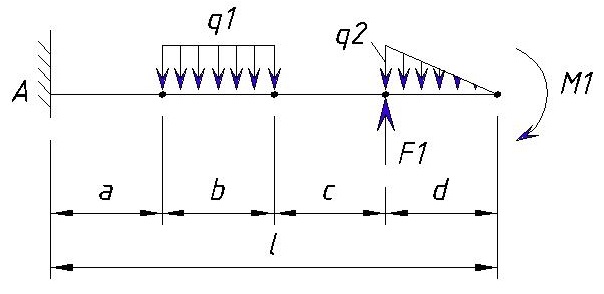
Мы уже рассматривали типовые эпюры консольной балки, теперь расскажем про построение эпюры консольной балки если на нее воздействуют сразу несколько нагрузок.

Чтобы легче было понять материал разберемся на примере:

Значения нагрузок:

q1=10 кН/м

q2=60 кН/м

F1=10 кН

M1=20 кН·м

Расстояния между точками равны т,е. a=b=c=d=1м

Опорные реакции

Построение эпюр, как правило, начинают с определения опорных реакций.

Определяем поперечную силу и изгибающий момент в точке А.

Для начала зададим направление опорных реакций

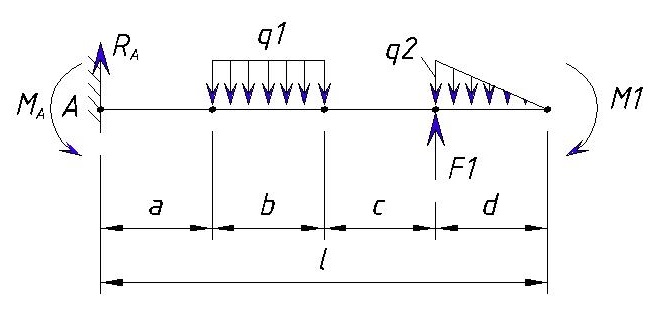
Т.к. система не подвижна, то сумма сил должна равняться нулю.

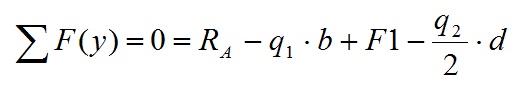
Нагрузки, направленные вверх, принимаются со знаком плюс.

Нагрузки, направленные вниз, принимаем со знаком минус.

Направление Ra мы приняли вверх. Если в процессе решения уравнение значение Ra будет отрицательным, значит она направлена в другую сторону.

В уравнении уравновешивающих сил вдоль оси Y изгибающий момент M1 не присутствует. Да и в консольной балке момент, приложенный на любом участке балки, не влияет на поперечные силы. Только если будет как минимум еще одна опора момент повлияет на опорную реакцию и, соответственно, на поперечные силы, но в данном уравнении его все равно не будет.

Из этого уравнения вычисляем значение опорной реакции Ra:

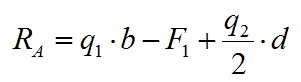
Подставляем значения нагрузок и вычисляем значение опорной реакции Ra:

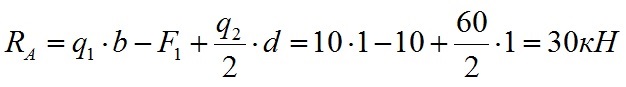
Мы вычислили значение опорной реакции Ra. Значение положительное, значит направление нагрузки мы назначили правильно.

Далее составляем уравнение равновесия изгибающих моментов вокруг точки A. Если система неподвижна, сумма моментов вокруг любой точки равна нулю.

Уравнение равновесия моментов вокруг точки A для нашего примера будет выглядеть следующим образом:

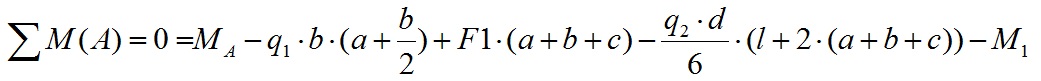
Значение момента от действия силы вокруг определенной точки равно произведению этой силы на расстояние от заданной точки до центра приложения нагрузки. Чтобы было понятно какой изгибающий момент создает каждый вид нагрузки, давайте рассмотрим их по отдельности.

Изгибающий момент M1 влияет на опорный момент вне зависимости от того где он приложен, т.е. не важно приложен он в середине балки или на конце на опорный момент он будет влиять одинаково.

Сосредоточенная сила F1 создает изгибающий момент равный произведению его значения на плечо (расстояние от рассматриваемой точки до точки приложения силы). Т.е. чем больше плечо, тем больший изгибающий момент создает сила F1.

Равномерно-распределенная сила q1 создает момент, равный произведению этой нагрузки на длину приложения этой нагрузки и на плечо (расстояние от рассматриваемой точки до центра равномерно-распределенной нагрузки). Т.е. мы можем представить распределенную нагрузку как сосредоточенную в центре этой нагрузки и умножить это значение на плечо.

Переменная нагрузка сила q2 создает момент, равный произведению половины произведения этой нагрузки на длину приложения и на плечо (расстояние от рассматриваемой точки, до центра приложения нагрузки, который расположен на расстоянии 1/3 от общей длины приложения этой нагрузки, ближе к максимальному значению). В данном примере это выглядит так:

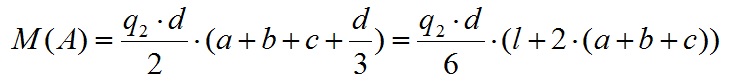
Из этого уравнения мы можем вычислить значение опорного момента Ma:

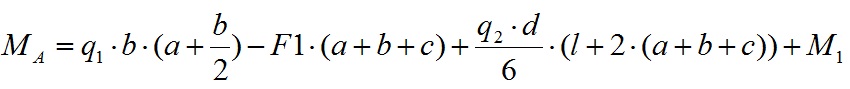
Подставляем значения и вычисляем значение опорного момента в точке A:

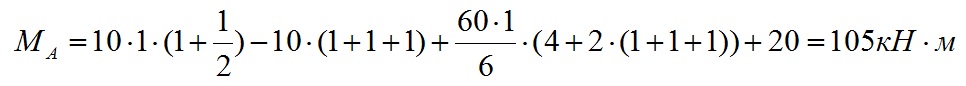
Мы вычислили значение опорного момента Ma. Значение опорного момента Ma положительное, поэтому направление действия момента задано правильно.

Назначение контрольных точек

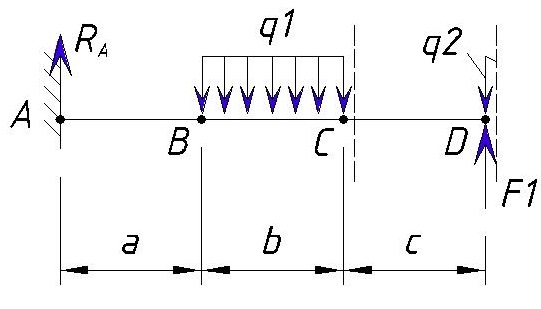
Для начала определяем контрольные точки на балке. 2-е точки естественно будут начало и конец балки, а промежуточные точки будут места приложения нагрузок (в случае равномерно-распределенной или переменной нагрузки точками будут начало и коней приложения нагрузки). Рассмотрим на примере разделение консольной балки на участки:

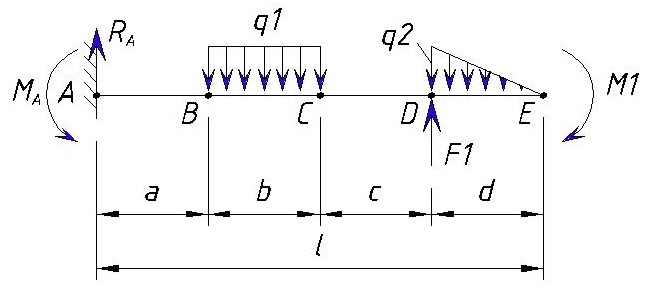
Точку заделки мы обозначили буквой «А».

Далее ближайшая точка «В» — это место приложения начала равномерно-распределенной нагрузки q1. Расстояние между точкой «А» и «B» равно a.

Далее следующая точка «С» — это конец приложения равномерно-распределенной нагрузки q1. Расстояние между точкой «B» и «C» равно b.

Следующая точка «D» — это начало приложения переменной нагрузки q1 и точка приложения силы F1. Расстояние между точкой «C» и «D» равно c.

Следующая точка «E» — это конец приложения переменной нагрузки q1, точка приложения изгибающего момента M1 и конец балки. Расстояние между точкой «D» и «E» равно d.

Построение эпюры Q (поперечной силы)

Разбиваем балку на участки между контрольными точками, т.е. участок AB (между точками A и B), участок BC (между участками B и C) и т.д.

В нашем примере у нас есть 4 участка: AB, BC, CD,DE.

Эпюру поперечных сил Q мы можем строить перемещаясь от точки А до точки E, рассчитывая значения в каждой точке, либо наоборот от точки E до точки A. В данном примере мы будем следовать от точки A, до точки E.

На каждом участке мы определяем значения и строим эпюру. По горизонтальной оси будут откладываться координаты, по вертикали откладываются значения (вверх от консольной балки откладываются положительные значения, вниз откладываются отрицательные значения).

Далее необходимо соединить эти точки линиями. Все точки, кроме точек между началом и концом переменной нагрузки, соединяются по прямой линии. Переменная нагрузка от начала, до конца соединяется изогнутой линией, напоминающей гиперболу, изогнутой вниз если нагрузка возрастает к месту заделки (если заделка слева) и изогнутой вверх если нагрузка к месту заделки спадает.

Правило знаков для построения эпюры Q

Если внешняя нагрузка, приложенная к рассматриваемой части, стремится повернуть сечение на заданном участке по часовой стрелке, то значение будет положительным и откладывается вверх.

Если внешняя нагрузка стремится повернуть сечение на заданном участке против часовой стрелки, то значение будет отрицательным и откладывается вниз.

Точка, вокруг которой поворачивают заданный участок не обязательно точка закрепления. Это точка, которую мы задаем на заданном участке в направлении к которой мы строим эпюру: если мы строим эпюру слева направо (как в данном примере), то это самая правая точка на заданном участке, если строим эпюру справа налево, то это самая левая точка на заданном участке.

Определяем напряжения Q на участке AB.

Рассмотрим участок AB. При рассмотрении участка AB мы как бы отбрасываем все остальные участки и не учитываем их на данном этапе. Кроме этого вначале мы не учитываем силы, приложенные в точке B.

Значение поперечной силы в точке А равно значению опорной реакции Ra, которое мы вычислили ранее. Не забываем про правило знаков — если сила стремится повернуть рассматриваемый участок по часовой стрелке, то значение принимается со знаком плюс, если против часовой, то со знаком минус. Мы как-бы откидываем закрепление балки в точке А, заменив ее силой Ra, и закрепляем в точке B. Сила Ra стремится повернуть участок вокруг точки B по часовой стрелке, поэтому Ra принимается со знаком плюс.

С правилом знаков поначалу возникают некоторые проблемы. Точка, вокруг которой мы мысленно вращаем данный участок, это не точка закрепления балки, а точка на участке, который мы в данный момент рассматриваем. Если мы строим эпюру слева направо (как в данной примере), это это будет самая правая точка, на рассматриваемом участке. Если строим эпюру справа налево, то это будет самая левая точка, на рассматриваемом участке.

Далее мы рассматриваем участок от точки А, до точки B, но при этом не учитываем нагрузки, которые приложены в самой точке B.

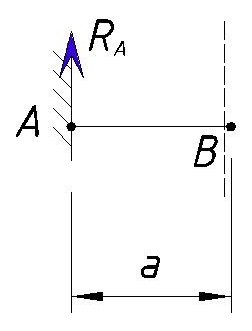
Пунктирной линией на рисунке обозначен участок, который мы рассматриваем.

На данном участке нет поперечных сил, кроме Ra, поэтому

Т.е. мы пока не учитываем силы, которые справа от этой точки и сила которая приложена именно в этой точке. Естественно силы, приложенные правее правее точки B влияют на значение поперечных сил на данном участке и они сейчас выражены в опорной реакции Ra. Как уже ранее выяснили сила Ra стремится повернуть сечение по часовой стрелке, поэтому Ra принимается со знаком «плюс» и откладывается вверх от оси.

Т.к. значение поперечной силы не изменилось, то эпюра Q на данном участке будет выглядеть как прямоугольник:

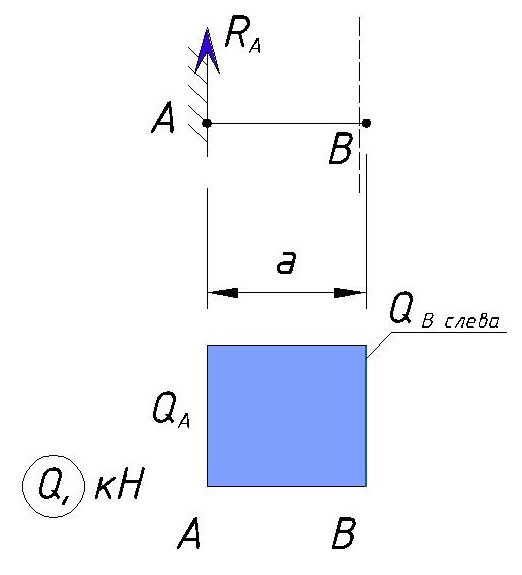
По вертикали мы откладываем значение поперечной силы, по горизонтали координаты балки.

Далее мы рассматриваем участок AB с учетом точки B, но принимаем участок не много правее точки B (на рисунке участок отсечен пунктирной линией)

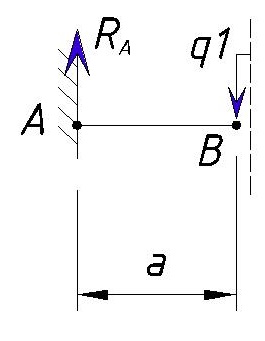
В точке B начинается равномерно-распределенная нагрузка q1, но мы рассматриваем участок правее точки как бы равный нулю, т.е. нагрузка q1 приложена в точке B, но еще имеет нулевую длину приложения нагрузки, поэтому она не изменяет значение поперечной силы в точке B.

Тут мы опять действуем согласно правилу знаков: точка, вокруг которой мы вращаем участок, находится не много правее точки B. Сила Ra стремится повернуть данный участок по часовой стрелке, поэтому она принимается со знаком «плюс».  Чтобы было проще при построении эпюры слева направо сила, направленная вверх всегда будет со знаком «плюс», а сила направленная вниз будет со знаком «минус».

Эпюра Q на данном участке получается следующая:

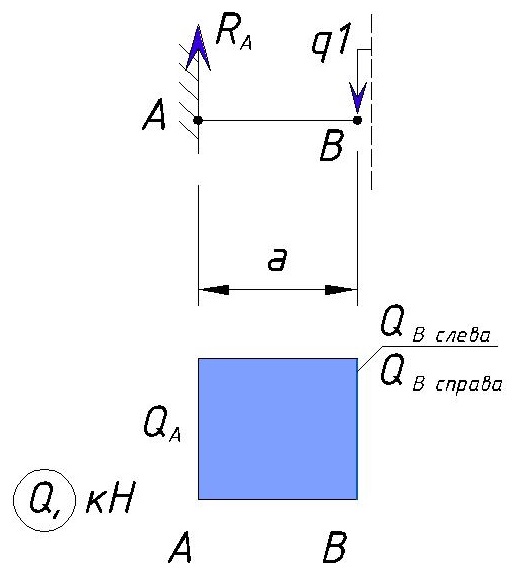
Определяем напряжения Q на участке BС.

Далее мы рассматриваем участок от точки B до точки C.

Пунктирными линиями я указал рассматриваемый участок.

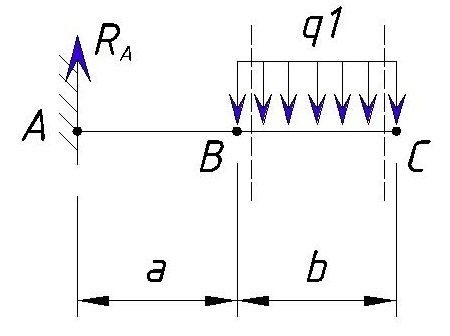
Значение поперечной силы в точке B справа мы уже вычислили ранее — это Q(B справа)=Ra=30 кН (именно значение, что справа).

На участке от точки B до точки C действует сила q1. По правилу знаков данная нагрузка стремится повернуть участок BC вокруг точки C против часовой стрелки, поэтому оно учитывается со знаком минус. Значение Q слева от точки C равно:

Строим эпюру поперечных сил на данном участке

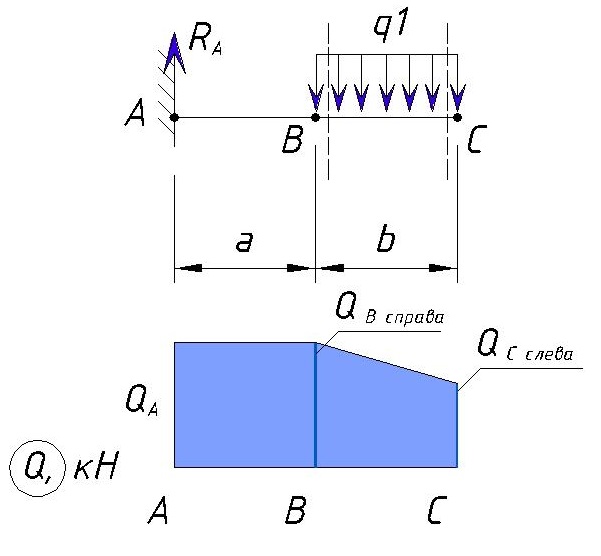
Далее рассматриваем участок BC, с точкой несколько правее точки C

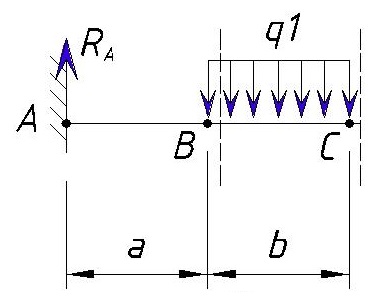
В точке C справа ничего не изменилось, поэтому

Эпюра Q на участке от A до C будет выглядеть следующим образом:

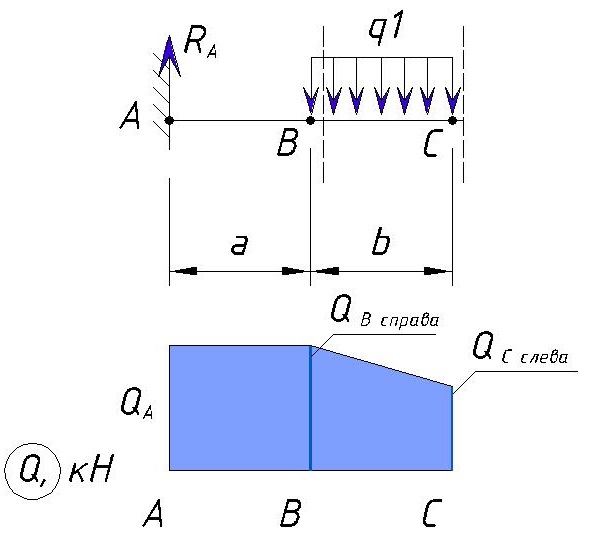
Определяем напряжения Q на участке СD.

Рассмотрим участок от точки C до точки D. Вначале рассматриваем участок левее точки D.

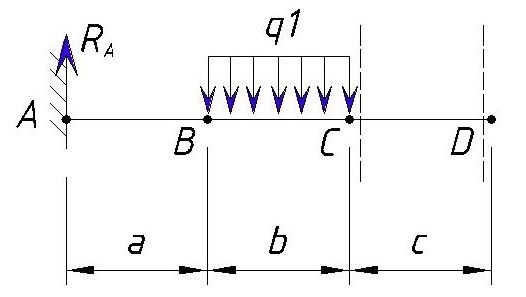
На данном участке нет поперечных сил, поэтому поперечная сила Q на данном участке не изменяется:

Эпюра на данном участке выглядит следующим образом:

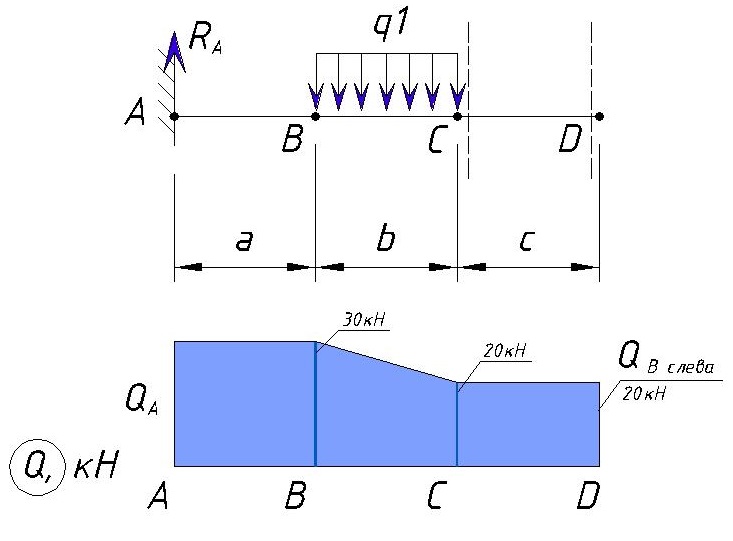
Далее рассмотрим участок с учетом сил, действующих в точке D

В точке D действует сосредоточенная сила F1 и начинает действовать переменная сила q2. Переменная сила q2 не влияет на поперечную силу в точке D т.к. она еще имеет нулевую длину приложения (правее этой точки она будет влиять, но это будет рассмотрено на участке DE). А сила F1 создает скачок поперечной нагрузки. Т.к. сила F1 стремится повернуть участок CD вокруг точки D по часовой стрелке сила F1 учитывается со знаком плюс (сила F1 вообще не может повернуть сечение вокруг точки D т.к. она приложена именно к этой точке, но тут точку вращения мы принимаем не много правее точки D т.к. это значение будет правее точки D).

Строим эпюру Q с учетом силы F1

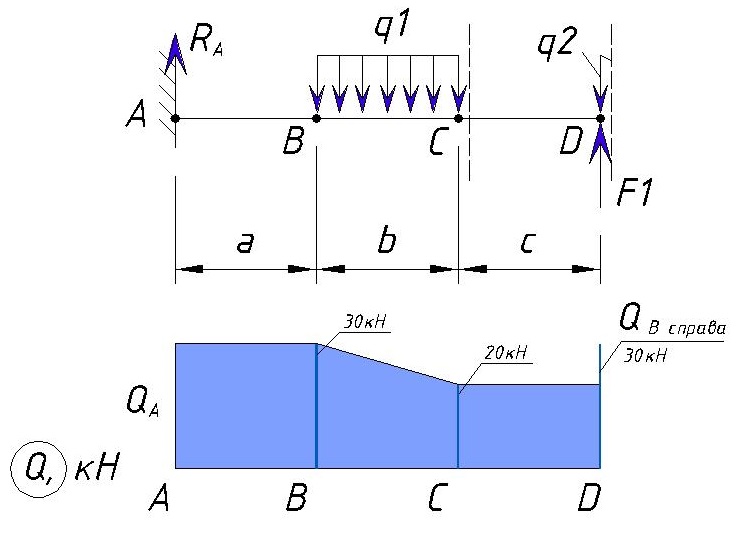
На эпюре мы видим скачок поперечной силы.

Определяем напряжения Q на участке DE.

Рассмотрим участок от точки D до точки E (слева)

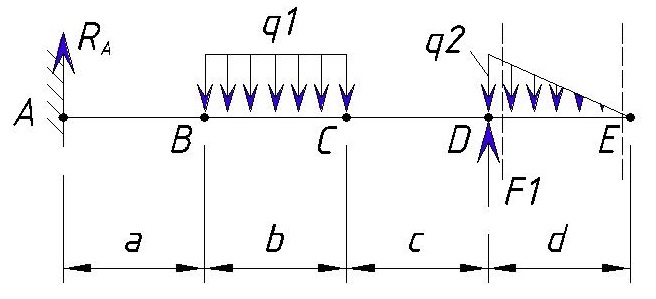
На участке от точки D до точки E приложена переменная нагрузка q2.

Определим значение Q в левее точки E. Сила q2 стремится повернуть сечение DE вокруг точки E против часовой стрелки, поэтому принимается со знаком минус. Значение поперечной силы в точке E слева равно:

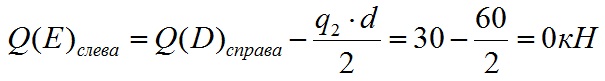
Эпюра на этом участке будет выглядеть как изогнутая линия т.к. переменная нагрузка с увеличением длины уменьшает свое влияние на поперечную силу и сводится к нулю в конце участка

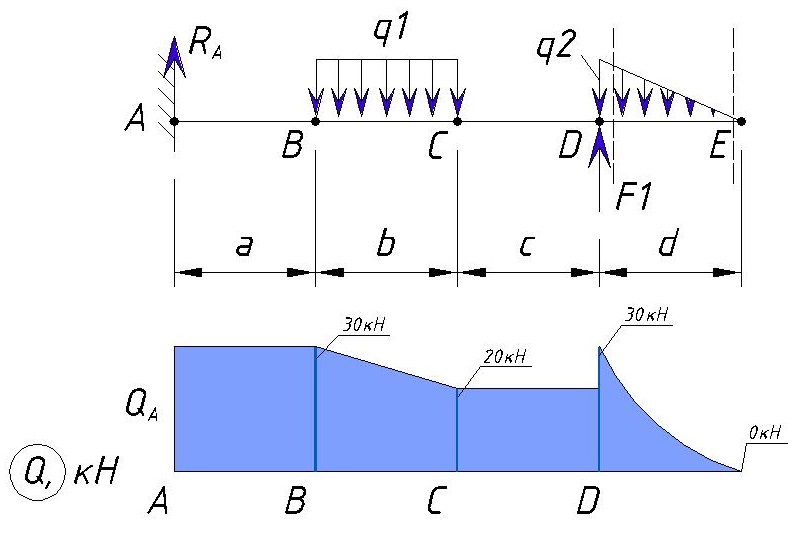
Далее рассматриваем участок DE с участком правее точки E

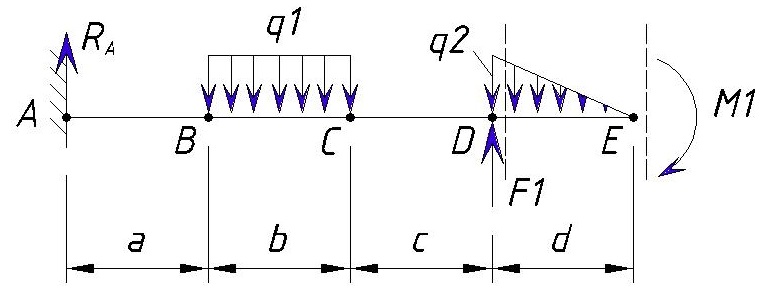
В точке E действует изгибающий момент M1, но он не влияет на поперечную силу, поэтому

Эпюра Q

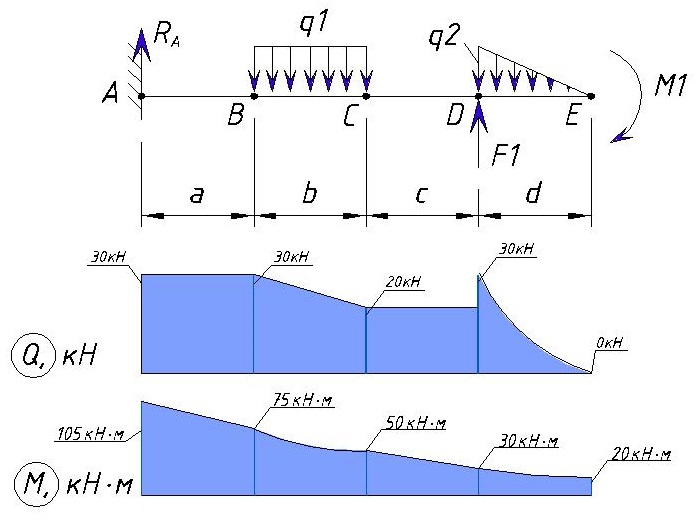
В итоге эпюра поперечной силы Q для данного примера выглядит следующим образом:

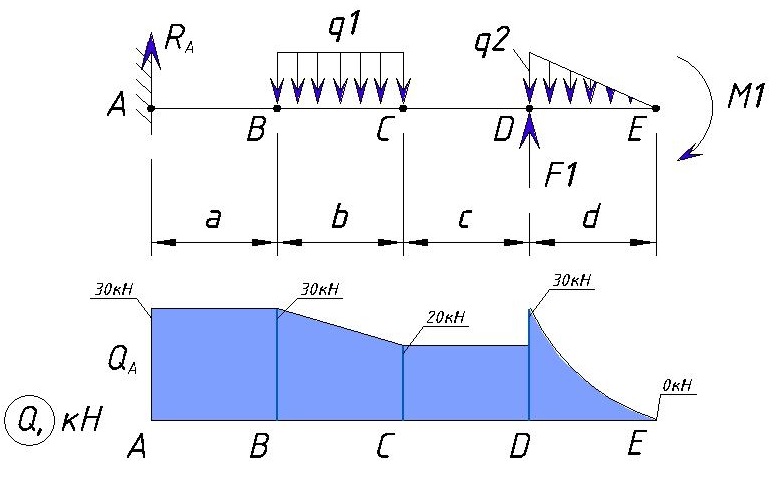
Как видим максимальная поперечная нагрузка, в данном примере, находится на участке от точки А до точки В, а также в точке D и равна Ra=30кН.

Вообще не во всех случаях обязательно рассматривать участок левее и правее заданной точки — только если в точке приложена сосредоточенная сила F эпюра Q осуществляет скачок, во всех остальных случаях Q(слева)=Q(справа). Я просто показал принцип построения эпюры.

В консольной балке напряжения Q в конце балки должны быть равны нулю. Конечно если на конце приложена сила F будет скачок напряжения, но  Q(справа) будет равна нулю.

Построение эпюры M (изгибающий момент)

Для построения эпюры М мы используем те же контрольные точки и те же участки, что мы использовали при построении эпюры Q.

Последовательно передвигаясь от точки А к концу балки мы вычисляем значения моментов в контрольных точках и соединяем их в график который и будет указывать изгибающий момент в любой точке балки.

Изгибающий момент вычисляется произведением силы или центра приложения силы на плечо.

Для сосредоточенной силы мы умножаем значение нагрузки на расстояние до рассматриваемой точки. На графике эпюра M от действия сосредоточенной силы имеет прямую линию.

Чтобы определить изгибающий момент от действия равномерно-распределенной нагрузки определяем расстояние до середины рассматриваемого участка равномерно-распределенной нагрузки, умножаем на длину рассматриваемого участка и на величину нагрузки. На графике эпюра М от действия равномерно-распределенной нагрузки напоминает изогнутую линию, гиперболу.

Для переменной нагрузки изгибающий момент определяем следующим образом: определяется центр приложения нагрузки (длина приложения нагрузки делится в соотношении 1/3-2/3, центр приложения нагрузки находится ближе к максимальной нагрузке), определяем длину от этой точки до рассматриваемой, умножаем на длину приложения нагрузки, и умножаем на половину от приложенной нагрузки (q).На графике эпюра М от действия переменной нагрузки также как и для равномерно-распределенной напоминает изогнутую линию, но с большим изгибом.

Приложенный момент в точке просто суммируется с вычисляемым изгибающим моментом от других нагрузок. В точке где приложен момент эпюра совершает скачок. Значение момента не умножается на расстояние, а остается неизменным по всей длине.

Правило знаков для построения эпюры M

Тут есть 2-а метода: метод которым пользуются строители и метод, которым пользуются машиностроители.

У строителей изгибающий момент считается положительным, если внешняя нагрузка приводит к растяжению верхних волокон и график откладываем вверх. Если внешняя нагрузка приводит к растяжению нижних волокон, то изгибающий момент считается отрицательным и график откладывается вверх. Т.е. график всегда откладывается в сторону растянутых волокон.

У машиностроителей все наоборот — положительное значение откладывается в сторону сжатых волокон.

Ни в том, ни в другом случае ошибки нет, просто разные методы и итоговые значения будут одинаковыми, только знаки противоположными.

Не могу с уверенностью сказать почему у строителей изгибающий момент направлен в сторону растянутых волокон. Возможно из-за того, что при данном рассмотрении эпюра моментов во многих случаях повторяет изгиб балки.

Мы будем рассматривать метод, которым пользуются строители.

Определяем напряжение M на участке AB

Также как и при определении эпюры Q, эпюру М также строим по тем же участкам.

Значение изгибающего момента в точке равно значению опорного момента Ma, который мы вычислили ранее.

Также как и при построении эпюры Q мы рассматриваем участок с точкой левее точки B и правее этой точки, но если при построении эпюры Q мы не учитывали изгибающие моменты, то при построении эпюры изгибающих моментов мы должны учитывать и изгибающие моменты, и поперечные силы.

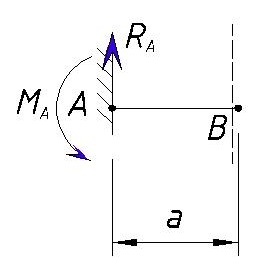
Изгибающий момент Ma стремится повернуть сечение вокруг точки B против часовой стрелки, а опорная реакция Ra по часовой стрелке. Теперь обратимся к правилу знаков. Изгибающий момент Ma стремится растянуть верхние волокна и сжать нижние, поэтому мы его учитываем со знаком плюс (читаем правило знаков для эпюры M). Опорная реакция Ra напротив стремится сжать верхние волокна и растянуть нижние, поэтому принимается со знаком минус. Напоминаю, что мы вращаем участок вокруг точки B, заделка в точке A заменена опорными реакциями Ra и Ma, т.е. если мы вместо заделки приложим эти силы, то система будет неподвижна.

Изгибающий момент в точке B слева будет равен:

На участке между точками A и B изгибающий момент изменяется прямолинейно т.к. на этом участке только реакция Ra изменяет значение, поэтому эпюра M на данном участке будет выглядеть так:

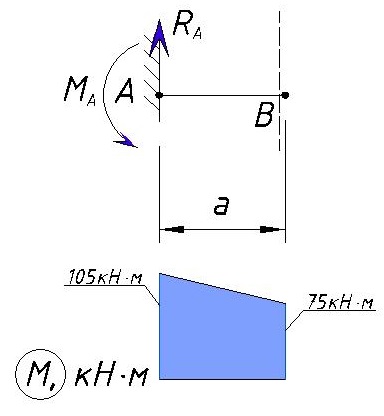
Теперь рассмотрим участок до точки B справа

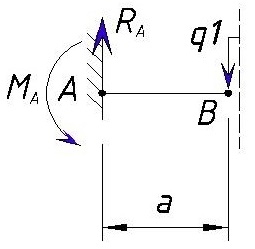
Тут добавляется равномерно распределенная нагрузка q1, но длина ее приложения еще равна нулю, поэтому она не влияет на изгибающий момент в точке B справа. Изгибающий момент справа от точки B буден равен значению слева от точки B.

Эпюра M выглядит следующим образом:

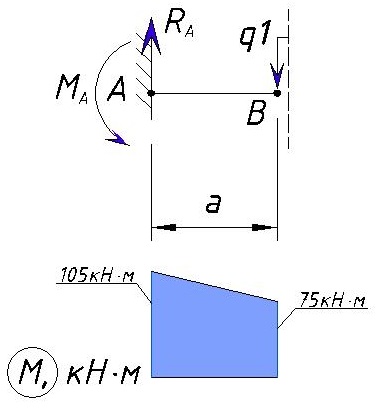
Определяем напряжение M на участке BС

Рассмотрим участок BC взяв участок без учета нагрузок в точке C (ну или как мы приняли левее точки C).

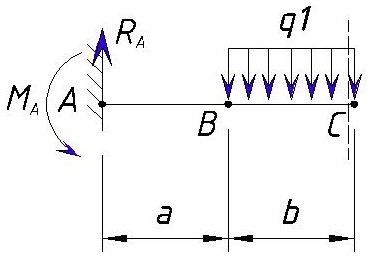
При вычислении изгибающего момента в точке C мы рассматриваем участок от точки A до С. Изгибающий момент в точке B вычисленный ранее является только значением в точке B и на точку C уже не влияет т.к. значение изгибающего момента изменяется в зависимости от плеча (расстояние от точки приложения нагрузки до рассматриваемой точки).

Изгибающий момент в точке С формируется из следующих составных:

1) Изгибающий момент Ma — опорная реакция в точке A. Значение изгибающего момента на изменяется от расстояния. Также как и для точки B значение изгибающего момента принимаем со знаком плюс т.к. он растягивает верхние волокна в точке C.

2) Опорная реакция Ra. Значение изгибающего момента в точке C напрямую зависит от плеча приложения нагрузки, поэтому в точке C опорная реакция Ra создает изгибающий момент в 2-а раза больше чем в точке B. Опорная реакция также сжимает верхние волокна, поэтому принимается со знаком минус.

3) Равномерно-распределенная нагрузка q1 создает изгибающий момент в точке C равный произведению этой нагрузки на длину ее приложения и на расстояние до центра ее приложения. По правилу знаков нагрузка q1 растягивает верхние волокна и принимается со знаком плюс.

Значение изгибающего момента в точки С слева равно:

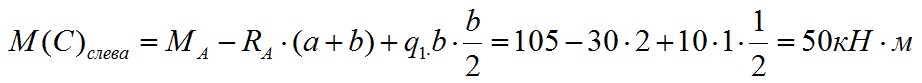
На участке действия равномерно-распределенной нагрузки эпюра M имеет изогнутую форму. Изгиб направлен в сторону действия нагрузки. Эпюра на участке от A до C имеет следующий вид:

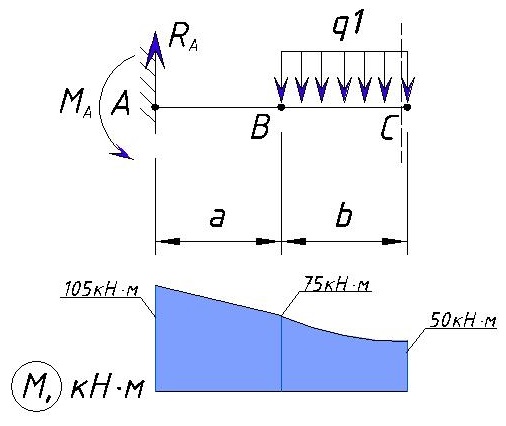
Теперь рассмотрим участок правее точки C

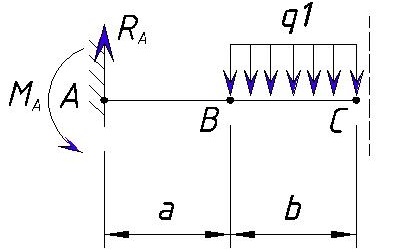
В принципе тут ничего не изменяется, новых нагрузок не появляется, расстояние (плечо) тоже остается тоже, поэтому эпюра с учетом этого участка выглядит также

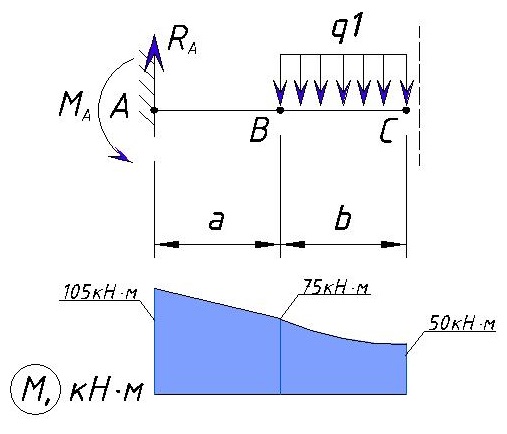
Определяем напряжение M на участке СD

Также рассматриваем участок слева от точки D

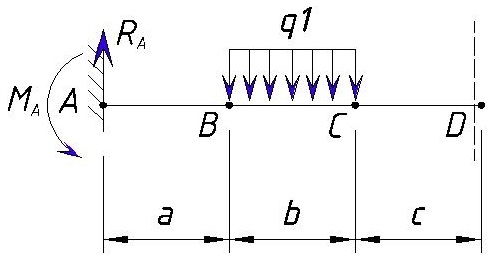
Изгибающий момент в точке D формируется из следующих составных:

1) Изгибающий момент Ma — опорная реакция в точке A. Значение изгибающего момента на изменяется от расстояния. Также как и для точки B значение изгибающего момента принимаем со знаком плюс т.к. он растягивает верхние волокна в точке D.

2) Опорная реакция Ra. Значение изгибающего момента в точке Dнапрямую зависит от плеча приложения нагрузки, поэтому в точке D опорная реакция Ra создает изгибающий момент в 3-и раза больше чем в точке B. Опорная реакция также сжимает верхние волокна, поэтому принимается со знаком минус.

3) Равномерно-распределенная нагрузка q1 создает изгибающий момент в точке D равный произведению этой нагрузки на длину ее приложения и на расстояние до центра ее приложения. По правилу знаков нагрузка q1 растягивает верхние волокна и принимается со знаком плюс.

Значение изгибающего момента в точки D слева равно:

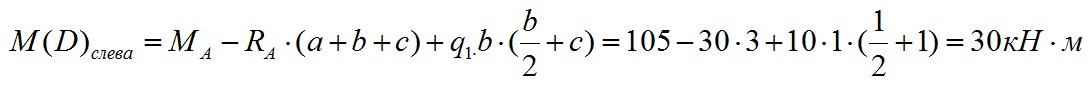
На участке CD нет никаких нагрузок, поэтому изменение напряжения M прямолинейно

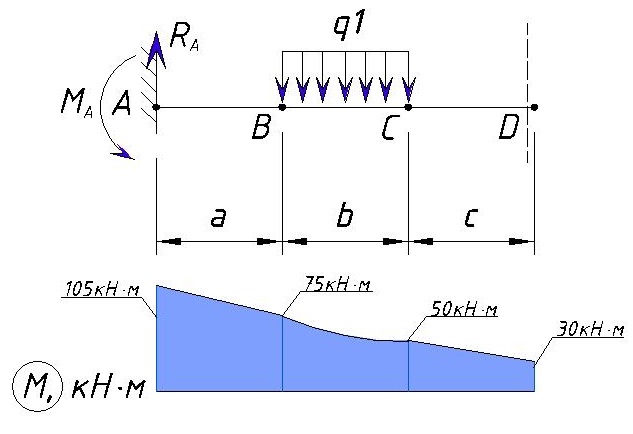
Рассмотрим точку D справа

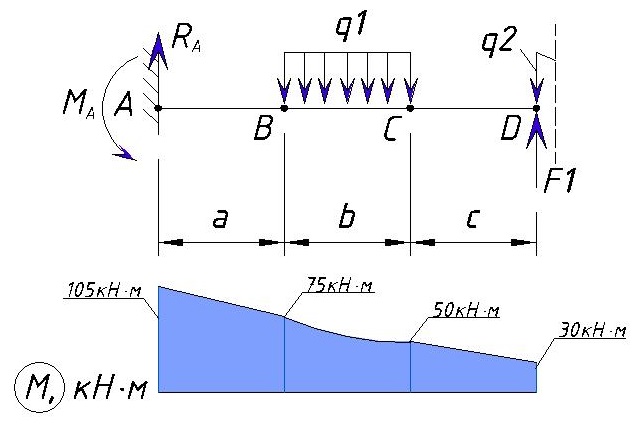
В точке D начинается приложение переменной нагрузки q2 и приложена сосредоточенная сила F1, но плечо приложения нагрузки еще равно нулю, поэтому значение изгибающего момента M в точке D справа не изменяется и равно значению слева от точки D.

Определяем напряжение M на участке DE

Рассматриваем участок слева от точки E

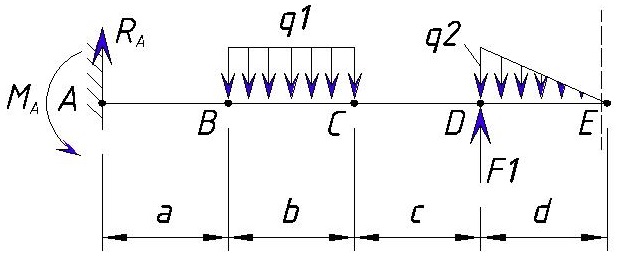
Изгибающий момент в точке E слева формируется из следующих составных:

1) Изгибающий момент Ma — опорная реакция в точке A. Значение изгибающего момента на изменяется от расстояния. Также как и для точки B значение изгибающего момента принимаем со знаком плюс т.к. он растягивает верхние волокна в точке E.

2) Опорная реакция Ra. Значение изгибающего момента в точке E напрямую зависит от плеча приложения нагрузки, поэтому в точке E опорная реакция Ra создает изгибающий момент в 4-ре раза больше чем в точке B. Опорная реакция также сжимает верхние волокна, поэтому принимается со знаком минус.

3) Равномерно-распределенная нагрузка q1 создает изгибающий момент в точке E равный произведению этой нагрузки на длину ее приложения и на расстояние до центра ее приложения. По правилу знаков нагрузка q1 растягивает верхние волокна и принимается со знаком плюс.

4) Сосредоточенная сила F1 создает изгибающий момент, равный произведению силы на плечо. Т.к. действие силы стремится сжать верхние волокна (напоминаю мы рассматриваем действие силы вокруг точки E), то изгибающий момент принимаем со знаком минус.

5) Переменная нагрузка q2 создает изгибающий момент, равный произведению половины от максимальной силы, на длину приложения и на расстояние от центра сил (точка находится примерно 1/3 участка приложения сил ближе к максимальной нагрузке) до рассматриваемой точки

Значение изгибающего момента в точки E слева равно:

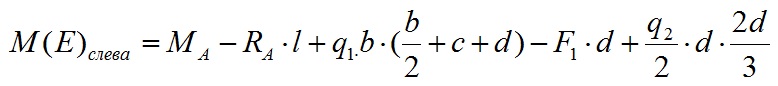
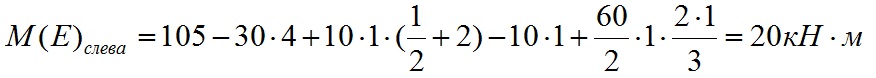
На участке DE изменение изгибающего момента не равномерно т.к. на этом участке имеется переменная нагрузка, эпюра имеет изогнутый вид

Теперь рассмотрим точку E с учетом приложенной к нему нагрузок (точка E справа)

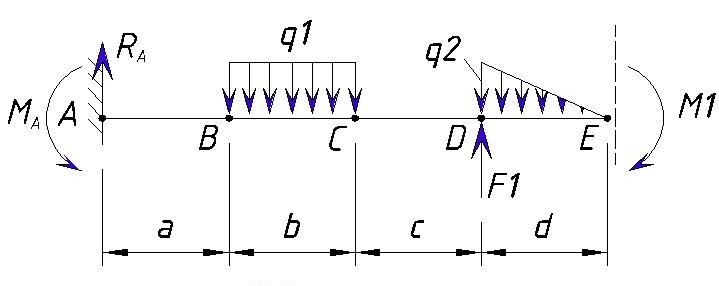
Тут добавляется момент M1. Действие изгибающего момента M1 стремится сжать верхние волокна поэтому мы принимаем его со знаком минус.

Значение изгибающего момента справа от точки E равно:

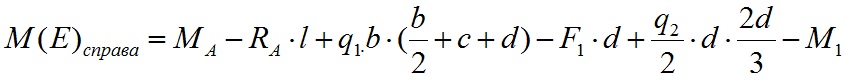
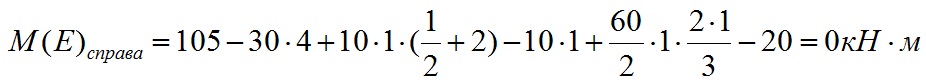
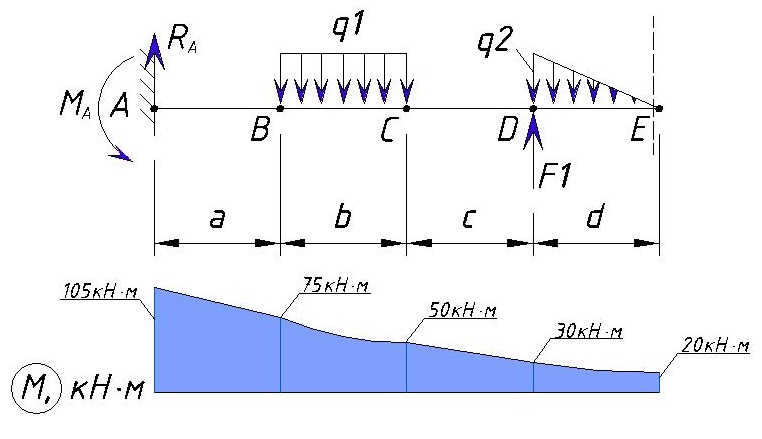
Действие изгибающего момента создает скачок в точке E. В итоге мы получаем такую эпюру изгибающих моментов для данного примера:

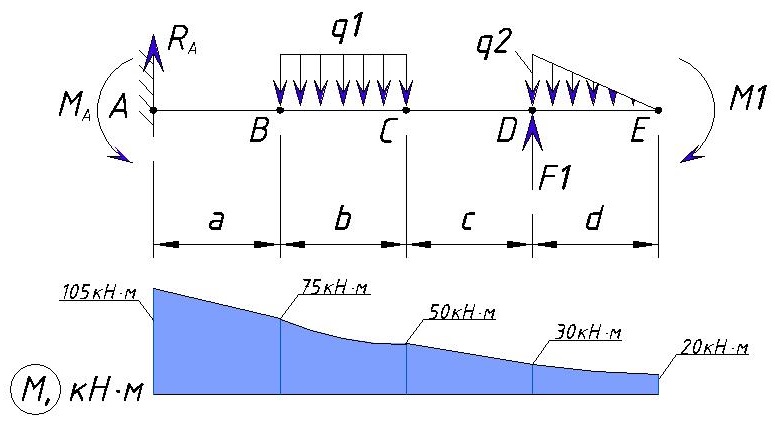
Значение изгибающего момента для консольной балки всегда равно нулю на свободном конце. Только если в конце балки приложен момент он будет отличатся на графике и будет равен значению этого момента, но изгибающий момент для E справа все равно будет равен нулю.

Также как и для эпюры Q не всегда обязательно рассматривать значения справа и слева от рассматриваемой точки. Только для точки в которой приложен изгибающий момент нужно рассматривать отдельно с учетом этого момента и без т.к. изгибающий момент создает скачок на эпюре моментов.

Эпюра Q и M

Покажем эпюры Q и M вместе чтобы увидеть где будут максимальные нагрузки

Надеюсь моя статья поможет в освоении азов сопротивления материалов.

Также ознакомитесь со статьей «Типовые эпюры консольной балки»