Прогон — это несущий элемент конструкции здания. Прогон поддерживает кровлю или пол и передает нагрузку на стены, балки или стропильную ферму.
В данной статье мы рассмотрим прогоны в промышленных зданиях из прокатных профилей, алгоритм прочностного расчета погона и балки, ответим на вопрос: «Какой профиль применять эффективнее?».
В СНиП II-23-81* (Стальные конструкции) расчет прогонов производился без учета действия бимомента, в СП 16.13330.2011 (Актуализированной редакции СНиП II-23-81*) появилось требование учета бимомента. Давайте разберемся в чем заключается учет бимомента при расчете балок и прогонов. Хотя новый СП пока носит рекомендательный характер, но вскоре он будет обязателен к применению.
При нагрузке профиля, расположенного под углом или при не равномерной нагрузке на профиль образуется изгибно-крутящий момент, который называется бимомент.
Очень подробно о расчете балок и прогонов с учетом бимомента расписано в книге «Строительная механика стержневых тонкостенных конструкций. Д.В.Бычков 1962.»
Расчет на изгиб согласно СНиП II-23-81*
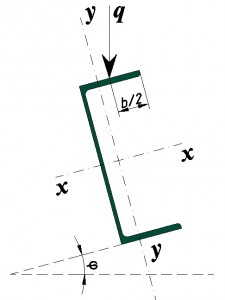
Рассмотрим следующий вариант нагружения:
Расчет на прочность при изгибе в 2-х главных плоскостях рассчитывается по формуле 38 (СНиП II-23-81*)
где:
Mx и My — значения изгибающих моментов вокруг оси x-x и y-y;
Jxn и Jyn — момент инерции сечения нетто вокруг оси x-x и y-y;
x и y — расстояние от центра масс до рассматриваемой точки;
Ry — расчетное сопротивление стали изгибу;
γс — коэффициент условий работы.
Т.к. максимальное значение напряжение возникает при максимальных значениях x и y, тогда:
Переместив Ry и γс в левую часть уравнения, получим формулу для проверки прочности элемента конструкции:
Для равномерно-нагруженной балки максимальный момент равен:
Для прогона расположенного под наклоном формулы для определения моментов будут выглядеть следующим образом:
Wx и Wy — моменты сопротивления сечения, определяются согласно ГОСТ-у на прокат.
Ry — расчетное сопротивление стали определяется исходя из принятой марки стали согласно приложению 1 СНиП II-23-81*.
Коэффициент условий работы (γс) задается согласно таблице 6 СНиП II-23-81 и, в зависимости от назначения балки, равен от 0,9 до 1,1.
При угле наклона равной нулю My будет равен нулю, а Мx примет максимальное значение.
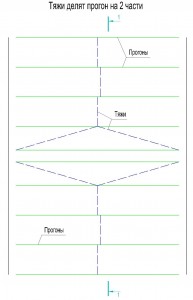
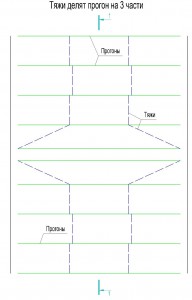
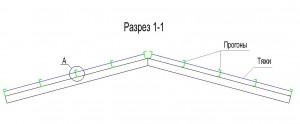
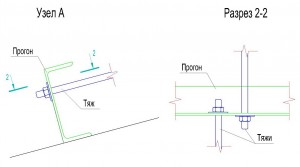
При увеличении угла наклона Mx уменьшается,а My увеличивается. В качестве прогона кровли обычно применяют швеллер, для него Wx имеет значение в несколько раз большее чем Wy. Для балки самым главным является значение Wx т.к. основной задачей балки является сопротивление изгибу в главной плоскости, но с увеличением угла изгибающий момент My увеличивается и это становится критическим фактором и необходимо увеличивать сечение. Для того, чтобы уменьшить момент My при больших уклонах применяют тяжи. Тяжи это элемент конструкции кровли, применяемый для уменьшения скатной составляющей момента. Схему расположения тяжей показана на следующих рисунках:
Верхний прогон тяжами не закрепляется т.к. нагрузка на него меньше, и покрытие кровли сможет обеспечить необходимую прочность. Тяжи делают из проката круглого сечения, в обычных ситуациях диаметр принимается 16 мм. Установка тяжей позволяет уменьшить изгибающий момент My.
Если тяжи делят прогон на 2-е части, то эпюра моментов будет соответствовать эпюре моментов 2-х пролетной балки, формула вычисления My будет выглядеть следующим образом:
Если тяжи делят прогон на 3-и части, то эпюра моментов будет соответсовать эпюре 3-х пролетной балки. Здесь есть интересный момент, при максимальном изгибающем моменте Mx изгибающий момент My не принимает своего максимального значения. В середине пролета My равен:
Максимальное значение My будет в точках крепления тяжей, здесь My принимает значение:
Изгибающий момент Mx в точке крепления тяжа примет значение :
Необходимо проверить оба условия.
Использование тяжей даже при угле 5 градусов дает прирост несущей способности 30 % по сравнению с прогоном без использования тяжей, поэтому их использование более чем оправданно. На более больших углах наклона использовать тяжи просто необходимо.
Расчет на изгиб согласно СП 16.133330.2011
Расчет на изгиб согласно СП 16.13330.2011 производится по формуле 43:
где:
Mx и My — значения изгибающих моментов вокруг оси x-x и y-y;
Jxn и Jyn — момент инерции сечения нетто вокруг оси x-x и y-y;
x и y — расстояние от центра масс до рассматриваемой точки;
Ry — расчетное сопротивление стали изгибу;
γс — коэффициент условий работы;
B — бимомент;
Jω-секториальный момент инерции;
ω-секториальная площадь;
1 — просто единица :).
Первые 2-а слагаемые мы уже разобрали, 3-е слагаемое это расчет напряжения в сечении при действии бимомента.
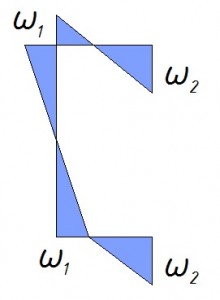
Бимомент возникает при скручивании профиля, но не обязательно необходимо прикладывать крутящий момент к профилю чтобы появился бимомент. При приложении нагрузки не через центр масс или при наклоне профиля возникают силы, скручивающие профиль. Если не учитывать эти силы, то профиль, особенно тонкостенный, может не выдержать нагрузки и закрутиться — это явление называют депланацией сечения. Мы разберем расчет прогона из швеллера при различных углах наклона.
Расчет бимомента B производим согласно методике, написанной в книге Д.В.Бычкова «Строительная механика стержневых тонкостенных конструкций».
Бимомент при равномерно-распределенной нагрузке вычисляется согласно формуле в Приложении 12 Д.В.Бычкова «Строительная механика стержневых тонкостенных конструкций»:
где:
α — это не угол, а коэффициент, определяемый согласно графика для определения расчетных изгибно-крутящих бимоментов (Приложение 12);
q — равномерно-распределенная нагрузка;
e — эксцентриситет приложения нагрузки относительно оси вращения;
l — длина стержня.
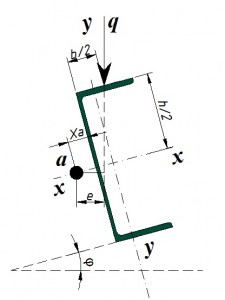
На следующем рисунке представлена схема нагружения швеллера:
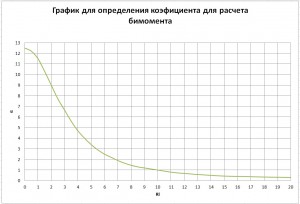
Коэффициент α определяется согласно следующему графику:
где:
l — длина балки;
R — коэффициент, который можно найти в Приложении 3, таблице 4 Руководства по подбору сечений элементов строительных стальных конструкций, это значение равно:
Перемножаем эти 2-а значения и по графику определяем значение α.
Нагрузку q разлагать по оси х-х и у-у не нужно.
Эксцентриситет для варианта представленного на рисунке вычисляется по формуле:
Jω-секториальный момент инерции и ω-секториальная площадь определяются согласно Приложению 3, таблице 4 Руководства по подбору сечений элементов строительных стальных конструкций.
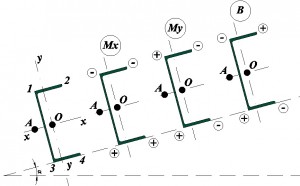
Точки расположения секториальных площадей показаны на следующем рисунке
Чтобы рассчитать балку на изгиб с учетом бимомента нам необходимо сделать расчет для 4-х точех. Для балки с равномерно-распределенной нагрузкой без тяжей знаки для составляющих формулы 43 СП 16.13330.2011 будут выглядеть следующим образом:
для точки 1:
для точки 2:
для точки 4:
Стоит отметить, что в данном случае бимомент разгружает профиль, т.е. если расчитывать без учета бимомента, то несущая способность профиля будет ниже.
Расчет прогона с учетом бимомента с раскреплением тяжами не рассмотрен т.к. этой методики в книге Бычкова нет, но я постараюсь найти методику расчета.
Также необходимо проверить прогоны на прочность при поперечной силе, расчет на прочность при действии сосредоточенной силы, расчет на прочность в опорном сечении и проверить прогиб. Методику расчета вы можете найди в моей предыдущей статье Расчет балки, но, как правило, самым критическим фактором является расчет на изгиб.
Итог:
В итоге мы видим что учет бимомента разгружает профиль, но пока новый СП 16.13330.2011 носит лишь рекомендательный характер, поэтому прогон необходимо считать по СНиП II-23-81*.
Для расчета прогонов я сделал программку в Excel, которая позволяет подобрать необходимый прогон из швеллера для кровли, скачать ее можно здесь 
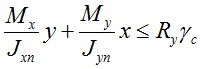
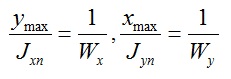
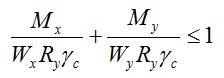
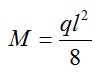
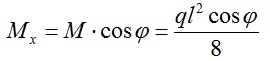
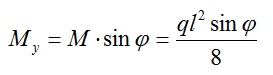
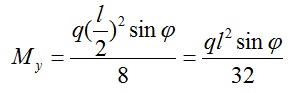
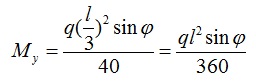
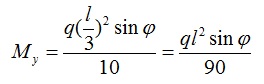
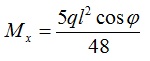
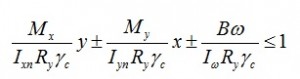
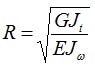
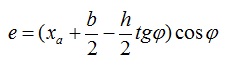
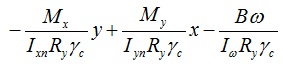
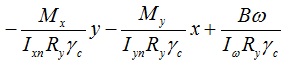
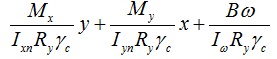
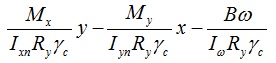
Большое спасибо за формулы. Смогу быстро провести расчеты. 🙂
все здорово но емель не работает
актуализируйте плиз. хотелось бы с автором пообщаться..
Большое спасибо, Денис! Доступное разъяснение по разным темам. Хотел бы спросить: у вас почему-то не учитывается ветровая нагрузка? Как по вашему мнению будет выглядеть расчёт прогона если он будет защемлён жёсткой заделкой? Заранее,спасибо.
Ветровую нагрузку лучше учитывать в 3D модели здания, кроме этого прогоны обычно не считают на ветровую нагрузку т.к. горизонтальные усилия в каркасе воспринимает система связей и ригелей.
А насчет жесткой заделки я не совсем понял — как вы собираетесь жестко закрепить прогон? Можно конечно приварить к балке и это будет жесткое закрепление, но в тоже время вы создаете закручивающий момент в балке, что не очень хорошо.
Если вы считаете балки с жестким закреплением, то лучше считать ее в составе рамы с учетом ветровых нагрузок либо создать 3D модель здания.
Здравствуйте, Денис. Иногда задаюсь таким глупым вопросом, почему прогоны ставят «спинкой» в сторону ската, а не наоборот. Каюсь, Бычкова не осилил)
Ув. Денис! Не совсем понятно как приняты знаки для составляющих формулы 43 СП16. Объясните пожалуйста подробнее.
Добрый день, Денис! Еще раз прошу объяснить как приняты правила знаков для расчета с учетом бимомента.
Денис, ваш расчет для 3-ей точки проверьте. Там бимомент не разгружает а догружает! Вы где-то ошиблись со знаком!!! Саш, надо добивать этот вопрос:)
В том то и дело! Но правило знаков в данной статье принято не так как в пособиях, поэтому и вопрос о правилах знаков.
Отличная статья!
Большое спасибо!
Вопрос немного не по теме. Скажите, пожалуйста, если к прогонам из прокатных профилей крепятся сэндвич-панели или профнастил с помощью саморезов, как учесть ослабление верхнего пояса профиля отверстиями под саморезы.
В данном случае можно не учитывать ослабление. Верхний пояс сжат. Отверстие будет заполнено саморезом, металл которого как правило прочнее прогона.
Швеллер развернуть на 180 градусов. Так профиль лучше работает в кармане н чего не скапливается.
Вы правы. Только в этом случае закрепить нужно будет не много по другому. А вообще там влаги то и не должно быть.
Добрый день Денис, при расчете на поперечную силу как учитывать угол наклона фи, или не надо учитывать?
Добрый день! Не понятно назначение знаков для бимомента. Для точки 3 с учетом бимомента усилие больше чем без него.
Почему при двухпролетной схеме с тяжом по середине Момент равен ql квадрат/32, если всю жизнь на средней опоре он был ql квадрат/8 ?